Understanding KMP algorithms

The core the KMP algorithm is the calculation of next array. Before looking into how to calculate next array, it is better to understand what to deal with string comparison between text and pattern.

in the context of brute force to solve the problem "find pattern in text", each time there is a mismatch between text[i+k] and pattern[k], pointer to text is set to i+1, and pointer to pattern reset to 0, until find a match(k == pattern.length), or i+k> tet.length, there is no pattern in text.

This naive approach wastes a lot comparison that is unnecessary, next array in KMP is trying to improve this mismatch-comparison situation. everytime there is a mismatch(j as the index), pattern is moved toward text end by LEN, this LEN means that there is a substring pattern[0..LEN] matches PATTERN[j-LEN..j-1], so that it can bypass unnecessary comparison.

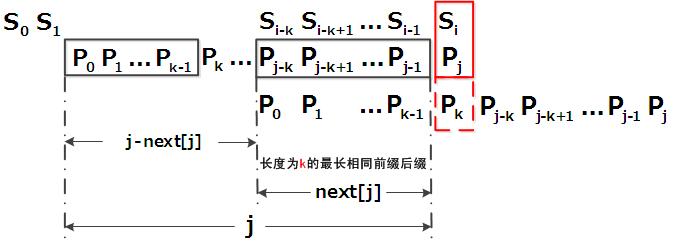
the LEN is next[j] : there is a length next[j] substring in pattern which appears in the begin and end of pattern(prefix and suffix).

the relationship between next array and max prefix-suffix is that during KMP algorithm, there is no need to consider current mismatch char, and there is no need to keep last max prefix-suffix, cause if match, the algorithm return. so the values in max prefix-suffix is shift right by one.

to Calculate max prefix-suffix array.

int[] max = new int[target.length()];
max[0] = 0;
for(int i=1; i< target.length(); i++){
     int k = max[i-1];
     while(k>0 && target.charAt(k) != target.charAt(i)) k = max[k-1];
     max[i] = target.charAt(k) == target.charAt(i) ? k+1 : k;
}

Calculate the next array is relatively simple. say we already know next[0..j], where next[j]==k(there is a substringP[0..k-1], length k, is a prefix-suffix, P[j] not included), to calculate next[j+1]:

1. if P[k] == P[j], next[j+1] = next[j]+1 = k+1;
2. if P[k] != P[j], we need to trace back to k == next[k], until
   1. P[next[k]] == P[j], then P[j] = next[k] +1;
   2. K == -1, P[j] == 0; where -1 is next[0];

int[] next = new int[N]; // N is pattern size;
next[0] = -1;
int k =-1;
int j=0;
while(j < N-1){
  if(k==-1 || P[k] == P[j]){
    ++k; ++j;
    next[j] = k;
  }else{
    k = next[k];
  }
}